 class HCL_TRCG_d : public HCL_TrustRegionSolver_d
class HCL_TRCG_d : public HCL_TrustRegionSolver_d  class HCL_TRCG_d : public HCL_TrustRegionSolver_d
class HCL_TRCG_d : public HCL_TrustRegionSolver_d The class HCL_TRCG_d is an implentation of the Steihaug-Toint algorithm for approximately solving the trust region subproblem
| | HCL_TRCG_d ( char * fname = NULL ) Usual constructor; optionally takes the name of a file from which to read algorithmic parameters |
| | Parameters () const The method Parameters returns the parameter table of the algorithm |
| | SetScaling ( HCL_LinearOp_d * S, HCL_LinearSolver_d * lsolver=NULL ) SetScaling defines a new inner product in terms of a symmetric, positive definite operator S: <x,y> = (x,Sy) |
| | UnSetScaling () UnSetScaling returns the inner product to the default. |
| | Solve ( const HCL_LinearOp_d & B, const HCL_Vector_d & g, HCL_Vector_d & p ) The method Solve attempts to compute an approximate solution of the trust region subproblem defined by the inputs of the method |
| | Write ( ostream & str ) const Prints description of the object |
The class HCL_TRCG_d is an implentation of the Steihaug-Toint algorithm for approximately solving the trust region subproblem. This algorithm is based on using the conjugate gradient (CG) method to compute the Newton step, with modifications for handling the case in which the approximate step, as computed by CG, leaves the trust region, and the case in which negative curvature is encountered. Note, in particular, that in spite of the use of CG, the linear operator defining the quadratic model is not assumed to be positive definite.For more information about the underlying algorithm, see
"The conjugate gradient method and trust regions in large scale optimization" by Trond Steihaug, SIAM J. Numer. Anal. Vol. 20, No. 3, 626--637
![]() double Tol
double Tol
![]() int MaxItn
int MaxItn
![]() int DispFlag
int DispFlag
![]() int DispPrecision
int DispPrecision
![]() int DispFreq
int DispFreq
![]() double MinStep
double MinStep
![]() double MaxStep
double MaxStep
![]() double Multiplier
double Multiplier
ParameterName = value
or
TRSolver::ParameterName = value
The second form allows the same file to contain parameters for more than one algorithm to be given in the same file. For example, one can entries such as
UMin::DispFlag = 2 TRSolver::DispFlag = 1
which set the display flags for the minimization algorithm and the trust region solver to different values.
![]() virtual Table& Parameters() const
virtual Table& Parameters() const
![]() virtual void SetScaling( HCL_LinearOp_d * S, HCL_LinearSolver_d * lsolver=NULL )
virtual void SetScaling( HCL_LinearOp_d * S, HCL_LinearSolver_d * lsolver=NULL )
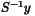 when needed.
when needed.
![]() virtual void UnSetScaling()
virtual void UnSetScaling()
![]() virtual void Solve( const HCL_LinearOp_d & B, const HCL_Vector_d & g, HCL_Vector_d & p )
virtual void Solve( const HCL_LinearOp_d & B, const HCL_Vector_d & g, HCL_Vector_d & p )
![]() virtual ostream& Write( ostream & str ) const
virtual ostream& Write( ostream & str ) const
alphabetic index hierarchy of classes

this page has been generated automatically by doc++
(c)opyright by Malte Zöckler, Roland Wunderling
contact: doc++@zib.de