 class HCL_ALFcnl_d : public HCL_Functional_d
class HCL_ALFcnl_d : public HCL_Functional_d  class HCL_ALFcnl_d : public HCL_Functional_d
class HCL_ALFcnl_d : public HCL_Functional_d HCL_ALFcnl_d implements an Augmented Lagrangian functional; it is intended for use with HCL_CMinAL_d
| | HCL_ALFcnl_d ( HCL_Functional_d * ff, HCL_Op_d * HH, HCL_Vector_d * l, double rho=1.0, HCL_LinearOp_d * SS=NULL ) Usual constructor |
| | Domain () const Domain space access. |
| | MaxStep ( const HCL_Vector_d & x, const HCL_Vector_d &dir) const MaxStep computes the longest vector from x in the direction dir that will lie in the domain of the functional, i |
| | Parameters () Access to parameter table |
| | Evaluate ( const HCL_Vector_d & x ) const Evaluate creates an "evaluation" object, which knows how to compute the function value and gradient at the given x |
| | Write ( ostream & str ) const Write prints out some useful information about the function. |
HCL_ALFcnl_d implements an Augmented Lagrangian functional; it is intended for use with HCL_CMinAL_d. Ifis a real-valued (objective) functional with domain
, and
is a (equality constraint) operator, then the augmented Lagrangian functional
is defined by
,
where
is the Lagrange multiplier and
is the penalty parameter. This class also allows the inner product on
to be scaled by a self-adjoint, positive definite operator
:
.
HCL_ALFcnl_d has the usual properties (methods) of the HCL_Functional_d base class; the documentation of the base class should be consulted for more information.
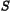 , used to scale the inner product on
the constraint space. The default value for the penalty parameter
is
, used to scale the inner product on
the constraint space. The default value for the penalty parameter
is 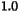 . Note that the penalty parameter can be updated using
the Parameters() method as follows:
Parameters().PutValue( "PenParam",newvalue );
. Note that the penalty parameter can be updated using
the Parameters() method as follows:
Parameters().PutValue( "PenParam",newvalue );
![]() virtual HCL_VectorSpace_d& Domain() const
virtual HCL_VectorSpace_d& Domain() const
![]() virtual double MaxStep( const HCL_Vector_d & x, const HCL_Vector_d &dir) const
virtual double MaxStep( const HCL_Vector_d & x, const HCL_Vector_d &dir) const
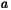 such that
such that 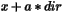 lies in the domain.
lies in the domain.
![]() Table& Parameters()
Table& Parameters()
![]() virtual HCL_EvaluateFunctional_d* Evaluate( const HCL_Vector_d & x ) const
virtual HCL_EvaluateFunctional_d* Evaluate( const HCL_Vector_d & x ) const
![]() virtual ostream& Write( ostream & str ) const
virtual ostream& Write( ostream & str ) const
alphabetic index hierarchy of classes

this page has been generated automatically by doc++
(c)opyright by Malte Zöckler, Roland Wunderling
contact: doc++@zib.de