 class HCL_Op_d : public HCL_Base
class HCL_Op_d : public HCL_Base  class HCL_Op_d : public HCL_Base
class HCL_Op_d : public HCL_Base HCL_Op_d is the base class for (presumably nonlinear) operators
| | Domain () const Domain space access |
| | Range () const Range space access |
| | MaxStep ( const HCL_Vector_d & x, const HCL_Vector_d &dir) const MaxStep computes the greatest a such that x + a*dir lies in the domain |
| | Image ( const HCL_Vector_d & x, HCL_Vector_d & y ) const Image computes the action of the operator on x, giving y |
| | ImageAdd ( const HCL_Vector_d & x, HCL_Vector_d & y, double a=1.0, double b=1.0 ) const ImageAdd computes 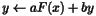
|
| | ImageAdd ( const HCL_Vector_d & x, const HCL_Vector_d & z, HCL_Vector_d & y, double a=1.0, double b=1.0 ) const ImageAdd computes 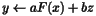
|
| | Deriv ( const HCL_Vector_d & x ) const Deriv computes the derivative, as an HCL_LinearOp_d, of the operator at x |
| | SecondDeriv ( const HCL_Vector_d & x ) const SecondDeriv computes the second derivative of the operator at a point |
| | Evaluate ( const HCL_Vector_d & x ) const Evaluate creates an evaluation object which knows how to compute the image, first derivative, and second derivative, along with all relevant adjoints, at a point |
| | CheckDeriv ( const HCL_Vector_d &, const HCL_Vector_d &, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const Check analytic derivative |
| | CheckDerivAdj ( const HCL_Vector_d &, const HCL_Vector_d &, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const CheckDerivAdj calls CheckDeriv to test the correctness of the derivative, and then calls the HCL_LinearOp_d method CheckAdj to test the correctness of its adjoint |
| | CheckSecondDeriv ( const HCL_Vector_d &, const HCL_Vector_d &, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const Check analytic second derivative |
| | CheckSecondDerivAdj ( const HCL_Vector_d &, const HCL_Vector_d &, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const CheckSecondDerivAdj calls CheckSecondDeriv to test the correctness of the second derivative, and then calls the HCL_LinearOp_d method CheckAdj to test the correctness of the three related adjoints |
| | DerivImage ( const HCL_Vector_d & x, const HCL_Vector_d & dx, HCL_Vector_d & dy ) const DerivImage computes the image of the derivative on dx, yielding dy |
| | DerivAdjImage ( const HCL_Vector_d & x, const HCL_Vector_d & dy, HCL_Vector_d & dx ) const DerivAdjImage computes the image of the adjoint of the derivative on dy, yielding dx |
| | DerivInvImage ( const HCL_Vector_d & x, const HCL_Vector_d & dy, HCL_Vector_d & dx ) const DerivInvImage computes the image of the inverse of the derivative on dy, yielding dx |
| | DerivInvAdjImage ( const HCL_Vector_d & x, const HCL_Vector_d & dx, HCL_Vector_d & dy ) const DerivInvAdjImage computes the image of the inverse of the adjoint of the derivative on dx, yielding dy |
| | Image1 ( const HCL_Vector_d & x, HCL_Vector_d & y ) const Image1 computes the image of the operator on x, yielding y |
| | Deriv1 ( const HCL_Vector_d & x ) const Deriv1 computes the derivative of the operator at x |
| | SecondDerivImage ( const HCL_Vector_d & x, const HCL_Vector_d & dx1, const HCL_Vector_d & dx2, HCL_Vector_d & dy ) const Writing  , this method computes , this method computes 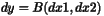
|
| | SecondDerivPartialAdjImage (const HCL_Vector_d & x, const HCL_Vector_d & dx1, const HCL_Vector_d & dy, HCL_Vector_d & dx2 ) const This method computes 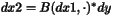
|
| | SecondDeriv1 ( const HCL_Vector_d & x ) const SecondDeriv1 computes the second derivative of the operator at x |
HCL_Op_d is the base class for (presumably nonlinear) operators. Such an operator maps one vector space into another, sayThe primary methods of this class are:
- Domain Returns a reference to the domain of the operator. This is used primarily for error-checking.
- Range Returns a reference to the range of the operator. This is used primarily for error-checking.
- Image Computes the action of the operator on a vector. Here is an example illustrating the use of Domain, Range, and Image:
void fcn( HCL_Op_d & F,HCL_Vector_d & x,HCL_Vector_d & y ) { if( x.Space() != F.Domain() || y.Space() != F.Range() ) // Error condition . . . F.Image( x,y ); // y <-- F(x) . . . }- ImageAdd Adds the image of the operator to the output vector.
- Deriv Creates the derivative of the operator at a point. This derivative is a linear operator
and this method constructs it as an HCL_LinearOp_d.
- SecondDeriv Creates the second derivative of the operator at a point. This derivative is a bilinear operator
and this method constructs it as an HCL_BiLinearOp_d.
- Evaluate Creates an "evaluation object" which knows the image and derivatives of the operator at a given point. The purpose of the evaluation object is to accommodate the common situation in which the computation of the image and derivatives involve some common intermediate calculations. The implementor of the operator can put these intermediate calculations in the evaluation object, so that they need only be done once at each point. The implementor of optimization algorithms should respect this by using Evaluate to get the image and/or derivatives instead of using Image, Deriv, and/or SecondDeriv.
In addition to the above methods, HCL_Op_d has a number of protected virtual functions that allow the user to avoid writing a distinct evaluation class if desired. If these methods, which include DerivImage, SecondDerivImage, and others, are over-ridden in a derived class, then the default Evaluate method can be used, which creates an instance of HCL_OpDefaultEval_d.
Defining operators is expected to be one of the main activities of users of HCL, since the many optimization problems involve operators in the definition of the objective function or constraints. As the last paragraph suggests, there are a number of ways to implement operators. These are described in detail in the report
"Implementing operators in HCL", Technical Report 99-22, Department of Computational and Applied Mathematics, Rice University, Houston, TX 77251-1892.
downloadable from the HCL home page.
![]() virtual void DerivAdjImage( const HCL_Vector_d & x, const HCL_Vector_d & dy, HCL_Vector_d & dx ) const
virtual void DerivAdjImage( const HCL_Vector_d & x, const HCL_Vector_d & dy, HCL_Vector_d & dx ) const
![]() virtual void DerivInvImage( const HCL_Vector_d & x, const HCL_Vector_d & dy, HCL_Vector_d & dx ) const
virtual void DerivInvImage( const HCL_Vector_d & x, const HCL_Vector_d & dy, HCL_Vector_d & dx ) const
![]() virtual void DerivInvAdjImage( const HCL_Vector_d & x, const HCL_Vector_d & dx, HCL_Vector_d & dy ) const
virtual void DerivInvAdjImage( const HCL_Vector_d & x, const HCL_Vector_d & dx, HCL_Vector_d & dy ) const
![]() virtual void Image1( const HCL_Vector_d & x, HCL_Vector_d & y ) const
virtual void Image1( const HCL_Vector_d & x, HCL_Vector_d & y ) const
![]() virtual HCL_LinearOp_d* Deriv1( const HCL_Vector_d & x ) const
virtual HCL_LinearOp_d* Deriv1( const HCL_Vector_d & x ) const
![]() virtual void SecondDerivImage( const HCL_Vector_d & x, const HCL_Vector_d & dx1, const HCL_Vector_d & dx2, HCL_Vector_d & dy ) const
virtual void SecondDerivImage( const HCL_Vector_d & x, const HCL_Vector_d & dx1, const HCL_Vector_d & dx2, HCL_Vector_d & dy ) const
 , this method computes
, this method computes 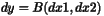 .
If this method and the related protected image methods are
implemented, then the default Evaluate method can be used.
The evaluation method will then be an instance of
HCL_OpDefaultEval_d. Note that either the pair
SecondDerivImage, SecondDerivPartialAdjImage or the method
SecondDeriv1 must be implemented to enable the use of the
default second derivative construction.
.
If this method and the related protected image methods are
implemented, then the default Evaluate method can be used.
The evaluation method will then be an instance of
HCL_OpDefaultEval_d. Note that either the pair
SecondDerivImage, SecondDerivPartialAdjImage or the method
SecondDeriv1 must be implemented to enable the use of the
default second derivative construction.
![]() virtual void SecondDerivPartialAdjImage(const HCL_Vector_d & x, const HCL_Vector_d & dx1, const HCL_Vector_d & dy, HCL_Vector_d & dx2 ) const
virtual void SecondDerivPartialAdjImage(const HCL_Vector_d & x, const HCL_Vector_d & dx1, const HCL_Vector_d & dy, HCL_Vector_d & dx2 ) const
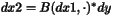 . If this method
and the related protected image methods are implemented, then the
default Evaluate method can be used. The evaluation method
will then be an instance of HCL_OpDefaultEval_d. Note
that either the pair SecondDerivImage,
SecondDerivPartialAdjImage or the method SecondDeriv1 must
be implemented to enable the use of the default second derivative
construction.
. If this method
and the related protected image methods are implemented, then the
default Evaluate method can be used. The evaluation method
will then be an instance of HCL_OpDefaultEval_d. Note
that either the pair SecondDerivImage,
SecondDerivPartialAdjImage or the method SecondDeriv1 must
be implemented to enable the use of the default second derivative
construction.
![]() virtual HCL_BiLinearOp_d* SecondDeriv1( const HCL_Vector_d & x ) const
virtual HCL_BiLinearOp_d* SecondDeriv1( const HCL_Vector_d & x ) const
![]() virtual HCL_VectorSpace_d& Domain() const
virtual HCL_VectorSpace_d& Domain() const
![]() virtual HCL_VectorSpace_d& Range() const
virtual HCL_VectorSpace_d& Range() const
![]() virtual double MaxStep( const HCL_Vector_d & x, const HCL_Vector_d &dir) const
virtual double MaxStep( const HCL_Vector_d & x, const HCL_Vector_d &dir) const
![]() virtual void Image( const HCL_Vector_d & x, HCL_Vector_d & y ) const
virtual void Image( const HCL_Vector_d & x, HCL_Vector_d & y ) const
![]() virtual void ImageAdd( const HCL_Vector_d & x, HCL_Vector_d & y, double a=1.0, double b=1.0 ) const
virtual void ImageAdd( const HCL_Vector_d & x, HCL_Vector_d & y, double a=1.0, double b=1.0 ) const
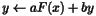 . (Note
that the scalars a and b are optional and default to 1.0.) It
does this by creating an evaluation object via Evaluate,
extracting the image, and deleting the evaluation object. This
method is defined in this (the base) class, so it need not be
redefined in concrete derived classes. However greater efficiency
may be obtained in some cases by overriding the default
implementation, through ``loop fusion''.
. (Note
that the scalars a and b are optional and default to 1.0.) It
does this by creating an evaluation object via Evaluate,
extracting the image, and deleting the evaluation object. This
method is defined in this (the base) class, so it need not be
redefined in concrete derived classes. However greater efficiency
may be obtained in some cases by overriding the default
implementation, through ``loop fusion''.
![]() virtual void ImageAdd( const HCL_Vector_d & x, const HCL_Vector_d & z, HCL_Vector_d & y, double a=1.0, double b=1.0 ) const
virtual void ImageAdd( const HCL_Vector_d & x, const HCL_Vector_d & z, HCL_Vector_d & y, double a=1.0, double b=1.0 ) const
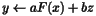 . (Note
that the scalars a and b are optional and default to 1.0.) It
does this by creating an evaluation object via Evaluate,
extracting the image, and deleting the evaluation object. This
method is defined in this (the base) class, so it need not be
redefined in concrete derived classes. However greater
efficiency may be obtained in some cases by overriding the
default implementation, through ``loop fusion''.
. (Note
that the scalars a and b are optional and default to 1.0.) It
does this by creating an evaluation object via Evaluate,
extracting the image, and deleting the evaluation object. This
method is defined in this (the base) class, so it need not be
redefined in concrete derived classes. However greater
efficiency may be obtained in some cases by overriding the
default implementation, through ``loop fusion''.
![]() virtual HCL_LinearOp_d* Deriv( const HCL_Vector_d & x ) const
virtual HCL_LinearOp_d* Deriv( const HCL_Vector_d & x ) const
![]() virtual HCL_BiLinearOp_d* SecondDeriv( const HCL_Vector_d & x ) const
virtual HCL_BiLinearOp_d* SecondDeriv( const HCL_Vector_d & x ) const
![]() virtual HCL_EvaluateOp_d* Evaluate( const HCL_Vector_d & x ) const
virtual HCL_EvaluateOp_d* Evaluate( const HCL_Vector_d & x ) const
![]() int CheckDeriv( const HCL_Vector_d &, const HCL_Vector_d &, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const
int CheckDeriv( const HCL_Vector_d &, const HCL_Vector_d &, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const
![]() int CheckDerivAdj( const HCL_Vector_d &, const HCL_Vector_d &, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const
int CheckDerivAdj( const HCL_Vector_d &, const HCL_Vector_d &, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const
![]() int CheckSecondDeriv( const HCL_Vector_d &, const HCL_Vector_d &, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const
int CheckSecondDeriv( const HCL_Vector_d &, const HCL_Vector_d &, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const
![]() int CheckSecondDerivAdj( const HCL_Vector_d &, const HCL_Vector_d &, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const
int CheckSecondDerivAdj( const HCL_Vector_d &, const HCL_Vector_d &, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const
alphabetic index hierarchy of classes

this page has been generated automatically by doc++
(c)opyright by Malte Zöckler, Roland Wunderling
contact: doc++@zib.de