 class HCL_BiLinearOp_d : public HCL_Base
class HCL_BiLinearOp_d : public HCL_Base  class HCL_BiLinearOp_d : public HCL_Base
class HCL_BiLinearOp_d : public HCL_Base HCL_BiLinearOp_d is the base class for bilinear operators
| | Domain1 () const Access to the domain of the first argument |
| | Domain2 () const Access to the domain of the second argument |
| | Range () const Access to the range |
| | Image ( const HCL_Vector_d & x, const HCL_Vector_d & y, HCL_Vector_d & z ) const Image computes the action of the operator on the pair (x,y), giving z |
| | Op1 ( const HCL_Vector_d & x ) const Op1 creates the linear operator B(x,.). Implemented in this class. |
| | Op2 ( const HCL_Vector_d & y ) const Op2 creates the linear operator B(.,y). Implemented in this class. |
| | Op3 ( const HCL_Vector_d & z ) const Access to the "partial adjoint" of the bilinear operator |
| | CheckAdj ( int Display = 1, double tol = 1000 ) CheckAdj invokes Op1, Op2, and Op3 at random points, and then tests them for consistency with their adjoints using the HCL_LinearOp_d method CheckAdj |
| | PartialAdjImage ( int i, const HCL_Vector_d & xy, const HCL_Vector_d & z, HCL_Vector_d & yx ) const The method PartialAdjImage implements the mappings 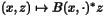 (i=1) and (i=1) and
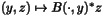 ( ( ) )
|
HCL_BiLinearOp_d is the base class for bilinear operators. A bilinear operator is of the formwhere X, Y, and Z are vector spaces and B(.,y) and B(x,.) are linear operators. Bilinear operators belong to the core of HCL because the second derivative of a nonlinear operator (at a point) is a bilinear operator.
The primary class methods are:
- Domain1 Returns a reference to the domain of the first argument of the operator.
- Domain2 Returns a reference to the domain of the second argument of the operator.
- Range Returns a reference to the range of the operator.
- Image Computes the action of the operator on a pair of vectors:
B.Image( x,y,z ); // z <-- B(x,y)- Op1 Creates the operator B(x,.). Note that this operator maps Y into Z.
- Op2 Creates the operator B(.,y). Note that this operator maps X into Z.
- Op3 Creates the operator x |--> B(x,.)'z as a linear operator with adjoint. Note that this operator maps X into Y.
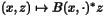 (i=1) and
(i=1) and
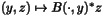 (
(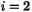 ). These methods are
implemented as error messages in this base class. If they are
over-ridden in a derived class, then the default implementations
of Op1, Op2, and Op3 may be used. Otherwise,
the implementor of the derived class is expected to over-ride
Op1, Op2, and Op3.
). These methods are
implemented as error messages in this base class. If they are
over-ridden in a derived class, then the default implementations
of Op1, Op2, and Op3 may be used. Otherwise,
the implementor of the derived class is expected to over-ride
Op1, Op2, and Op3.
![]() virtual HCL_VectorSpace_d& Domain1() const
virtual HCL_VectorSpace_d& Domain1() const
![]() virtual HCL_VectorSpace_d& Domain2() const
virtual HCL_VectorSpace_d& Domain2() const
![]() virtual HCL_VectorSpace_d& Range() const
virtual HCL_VectorSpace_d& Range() const
![]() virtual void Image( const HCL_Vector_d & x, const HCL_Vector_d & y, HCL_Vector_d & z ) const
virtual void Image( const HCL_Vector_d & x, const HCL_Vector_d & y, HCL_Vector_d & z ) const
![]() virtual HCL_LinearOp_d* Op1( const HCL_Vector_d & x ) const
virtual HCL_LinearOp_d* Op1( const HCL_Vector_d & x ) const
![]() virtual HCL_LinearOp_d* Op2( const HCL_Vector_d & y ) const
virtual HCL_LinearOp_d* Op2( const HCL_Vector_d & y ) const
![]() virtual HCL_LinearOp_d* Op3( const HCL_Vector_d & z ) const
virtual HCL_LinearOp_d* Op3( const HCL_Vector_d & z ) const
![]() int CheckAdj( int Display = 1, double tol = 1000 )
int CheckAdj( int Display = 1, double tol = 1000 )
alphabetic index hierarchy of classes

this page has been generated automatically by doc++
(c)opyright by Malte Zöckler, Roland Wunderling
contact: doc++@zib.de