 class HCL_EvalOpProductDomain_d : public HCL_EvaluateOp_d
class HCL_EvalOpProductDomain_d : public HCL_EvaluateOp_d  class HCL_EvalOpProductDomain_d : public HCL_EvaluateOp_d
class HCL_EvalOpProductDomain_d : public HCL_EvaluateOp_d This class represents an "evaluation" object that will be created by an HCL_OpProductDomain_d object to implement the image and derivatives of the operator at a point
| | Domain () const Domain returns a reference to the domain of the underlying operator |
| | ProductDomain () const ProductDomain returns a reference to the domain as a product vector space |
| | Range () const Range returns a reference to the range of the underlying operator. |
| | Image ( HCL_Vector_d & y ) const Image computes the image of the operator and assigns the result to y |
| | Deriv () const Deriv computes the derivative of the operator |
| | DerivRef () const DerivRef returns a reference to the derivative at this point |
| | PartialDeriv ( int i ) const PartialDeriv computes the partial derivative, with respect to the ith variable, as a linear operator |
| | PartialDerivRef ( int i ) const PartialDerivRef returns a reference to the partial derivative with respect to the ith variable |
| | SecondDeriv () const SecondDeriv computes the second derivative of the operator |
| | SecondDerivRef () const SecondDerivRef returns a reference to the second derivative at this point |
| | SecondPartialDeriv ( int i, int j ) const SecondPartialDeriv computes the second partial derivative, with respect to the ith and jth variables, as a bilinear operator |
| | SecondPartialDerivRef ( int i, int j ) const SecondPartialDerivRef returns a reference to the second partial derivative, with respect to the ith and jth variables |
| | Write ( ostream & str ) const Debugging information |
| | PartialDerivImage ( int i, const HCL_Vector_d & dx, HCL_Vector_d & dy ) const PartialDerivImage computes the image of the derivative on dx, yielding dy |
| | PartialDerivAdjImage ( int i, const HCL_Vector_d & dy, HCL_Vector_d & dx ) const PartialDerivAdjImage computes the image of the adjoint of the derivative on dy, yielding dx |
| | PartialDerivInvImage ( int i, const HCL_Vector_d & dy, HCL_Vector_d & dx ) const PartialDerivInvImage computes the image of the inverse of the derivative on dy, yielding dx |
| | PartialDerivInvAdjImage ( int i, const HCL_Vector_d & dx, HCL_Vector_d & dy ) const PartialDerivInvAdjImage computes the image of the inverse of the adjoint of the derivative on dx, yielding dy |
| | SecondPartialDerivImage ( int i, int j, const HCL_Vector_d & dxj, const HCL_Vector_d & dxi, HCL_Vector_d & dy ) const This method computes 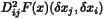
|
| | SecondPartialDerivPartialAdjImage ( int i, int j, int flag, const HCL_Vector_d & dxij, const HCL_Vector_d & dy, HCL_Vector_d & dxji ) const This method computes 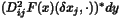 (flag==1) or
(flag==1) or 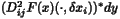 (flag==2)
(flag==2)
|
This class represents an "evaluation" object that will be created by an HCL_OpProductDomain_d object to implement the image and derivatives of the operator at a point. (The term "ProductDomain" refers to the fact that the operator in question is defined on a product space). Thus, ifis a nonlinear operator and
is a vector in the domain, then the evaluation object represents the triple
The purpose of having an evaluation object is to deal with the common situation in which the operator image and derivatives share some intermediate calculations. A typical implementation of such an operator involves defining an evaluation object whose constructor performs these intermediate calculations. The Image method then completes the computation of the operator image, while the PartialDeriv and SecondPartialDeriv methods complete the calculation of the derivatives.
The difference between HCL_EvaluateOp_d and HCL_EvalOpProductDomain_d is that the partial derivatives of the operator are available in the second case. Also, from the point of view of the implementor of the class, only the partial derivatives need be implemented; the class puts them together into the full derivative.
The operator image and derivatives should then be accessed through the ImageRef, DerivRef (or PartialDerivRef), and SecondDerivRef (or SecondPartialDerivRef) methods. These are methods implemented in the base class (i.e. they do not need to be redefined in a derived class). The ImageRef method invokes Image to get the image and returns a reference to it. On subsequent calls, ImageRef merely references the stored value. The other "reference" methods work in a similar fashion.
Here is a summary of the primary methods of this class:
- Domain Returns a reference to the domain of the underlying operator.
- Range Returns a reference to the range of the underlying operator.
- Image Computes the image of the operator at the point at which this object was created. Must be implemented by the creator of a concrete class.
- ImageRef Calls Image, if necessary, to compute the operator image, saves it, and returns it. Implemented in the base class.
- ImageAdd Adds the image of the operator to the output (as opposed to Image, which overwrites the output with the image).
- Deriv Computes the derivative of the operator, at the point at which this object was created, as an HCL_LinearOp_d. Must be implemented by the creator of a concrete class.
- DerivRef Calls Deriv, if necessary, to compute the derivatives, saves it, and returns a reference to it. Implemented in the base class.
- PartialDeriv Computes a partial derivative of the operator, at the point at which this object was created, as an HCL_LinearOp_d. Must be implemented by the creator of a concrete class.
- PartialDerivRef Calls PartialDeriv, if necessary, to compute a partial derivative, saves it, and returns a reference to it. Implemented in the base class.
- SecondDeriv Computes the second derivative of the operator, at the point at which this object was created, as a HCL_BiLinearOp_d. Must be implemented by the creator of a concrete class.
- SecondDerivRef Calls SecondDeriv, if necessary, to compute the second derivative, saves it, and returns a reference to it. Implemented in the base class.
- SecondPartialDeriv Computes a second partial derivative of the operator, at the point at which this object was created, as a HCL_BiLinearOp_d. Must be implemented by the creator of a concrete class.
- SecondPartialDerivRef Calls SecondPartialDeriv, if necessary, to compute the second derivative, saves it, and returns a reference to it. Implemented in the base class.
In addition to the above methods, HCL_EvaluateOp_d has a number of protected virtual functions that allow the user to avoid writing distinct derivative classes if desired. If these methods, which include PartialDerivImage, SecondPartialDerivImage, and others, are over-ridden in a derived class, then the default PartialDeriv and SecondPartialDeriv methods can be used, which create instances of HCL_OpDefaultPartialDeriv_d and HCL_OpDefaultSecondPartialDeriv_d.
The following report describes the implementation of operators in detail:
"Implementing operators in HCL", Technical Report 99-22, Department of Computational and Applied Mathematics, Rice University, Houston, TX 77251-1892.
A forthcoming report, "Implementing HCL functionals and operators on product spaces", will provide similar details about implementing operators on product spaces. This report should be available from the same source in early 2000.
![]() virtual void PartialDerivAdjImage( int i, const HCL_Vector_d & dy, HCL_Vector_d & dx ) const
virtual void PartialDerivAdjImage( int i, const HCL_Vector_d & dy, HCL_Vector_d & dx ) const
![]() virtual void PartialDerivInvImage( int i, const HCL_Vector_d & dy, HCL_Vector_d & dx ) const
virtual void PartialDerivInvImage( int i, const HCL_Vector_d & dy, HCL_Vector_d & dx ) const
![]() virtual void PartialDerivInvAdjImage( int i, const HCL_Vector_d & dx, HCL_Vector_d & dy ) const
virtual void PartialDerivInvAdjImage( int i, const HCL_Vector_d & dx, HCL_Vector_d & dy ) const
![]() virtual void SecondPartialDerivImage( int i, int j, const HCL_Vector_d & dxj, const HCL_Vector_d & dxi, HCL_Vector_d & dy ) const
virtual void SecondPartialDerivImage( int i, int j, const HCL_Vector_d & dxj, const HCL_Vector_d & dxi, HCL_Vector_d & dy ) const
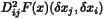 .
If this method and SecondPartialDerivPartialAdjImage are
implemented, then the default SecondPartialDeriv method
can be used; the second derivative will then be an instance of
HCL_OpDefaultSecondPartialDeriv_d.
.
If this method and SecondPartialDerivPartialAdjImage are
implemented, then the default SecondPartialDeriv method
can be used; the second derivative will then be an instance of
HCL_OpDefaultSecondPartialDeriv_d.
![]() virtual void SecondPartialDerivPartialAdjImage( int i, int j, int flag, const HCL_Vector_d & dxij, const HCL_Vector_d & dy, HCL_Vector_d & dxji ) const
virtual void SecondPartialDerivPartialAdjImage( int i, int j, int flag, const HCL_Vector_d & dxij, const HCL_Vector_d & dy, HCL_Vector_d & dxji ) const
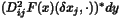 (flag==1) or
(flag==1) or 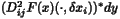 (flag==2). If this method and SecondPartialDerivImage are
implemented, then the default SecondPartialDeriv method
can be used; the second derivative will then be an instance of
HCL_OpDefaultSecondPartialDeriv_d.
(flag==2). If this method and SecondPartialDerivImage are
implemented, then the default SecondPartialDeriv method
can be used; the second derivative will then be an instance of
HCL_OpDefaultSecondPartialDeriv_d.
![]() virtual HCL_VectorSpace_d& Domain() const
virtual HCL_VectorSpace_d& Domain() const
![]() HCL_ProductSpace_d& ProductDomain() const
HCL_ProductSpace_d& ProductDomain() const
![]() virtual HCL_VectorSpace_d& Range() const
virtual HCL_VectorSpace_d& Range() const
![]() virtual void Image( HCL_Vector_d & y ) const
virtual void Image( HCL_Vector_d & y ) const
![]() virtual HCL_LinearOp_d* Deriv() const
virtual HCL_LinearOp_d* Deriv() const
![]() virtual const HCL_LinearOp_d& DerivRef() const
virtual const HCL_LinearOp_d& DerivRef() const
![]() virtual HCL_LinearOp_d* PartialDeriv( int i ) const
virtual HCL_LinearOp_d* PartialDeriv( int i ) const
![]() virtual const HCL_LinearOp_d& PartialDerivRef( int i ) const
virtual const HCL_LinearOp_d& PartialDerivRef( int i ) const
![]() virtual HCL_BiLinearOp_d* SecondDeriv() const
virtual HCL_BiLinearOp_d* SecondDeriv() const
![]() virtual const HCL_BiLinearOp_d& SecondDerivRef() const
virtual const HCL_BiLinearOp_d& SecondDerivRef() const
![]() virtual HCL_BiLinearOp_d* SecondPartialDeriv( int i, int j ) const
virtual HCL_BiLinearOp_d* SecondPartialDeriv( int i, int j ) const
![]() virtual const HCL_BiLinearOp_d& SecondPartialDerivRef( int i, int j ) const
virtual const HCL_BiLinearOp_d& SecondPartialDerivRef( int i, int j ) const
![]() virtual ostream& Write( ostream & str ) const
virtual ostream& Write( ostream & str ) const
alphabetic index hierarchy of classes

this page has been generated automatically by doc++
(c)opyright by Malte Zöckler, Roland Wunderling
contact: doc++@zib.de