 class HCL_FunctionalProductDomain_d : public HCL_Functional_d
class HCL_FunctionalProductDomain_d : public HCL_Functional_d  class HCL_FunctionalProductDomain_d : public HCL_Functional_d
class HCL_FunctionalProductDomain_d : public HCL_Functional_d HCL_FunctionalProductDomain_d is an abstract base class used to represents functionals defined on product spaces
| | Domain () const Domain space access |
| | ProductDomain () const Access to the domain, explicitly as a product vector space |
| | Evaluate ( const HCL_Vector_d & x ) const Evaluate creates an "evaluation" object, which knows how to compute the function value, gradient,and Hessian at the given x |
| | PartialGradient ( int i, const HCL_Vector_d & x, HCL_Vector_d & g ) const PartialGradient computes the gradient with respect to the ith component of the independent variable, at x |
| | HessianBlock ( int i, int j, const HCL_Vector_d & x ) const HessianBlock computes the (i,j) block of the Hessian operator |
| | CheckHessianBlock ( const HCL_Vector_d &, const HCL_Vector_d &, const HCL_Vector_d &, int i, int j, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const Check correctness of Hessian blocks |
| | CheckHessianBlock ( const HCL_Vector_d &, const HCL_Vector_d &, int ind, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const This version of CheckHessianBlock checks the ``pure'' (not mixed) second partial derivative using the usual central difference formula |
| | CheckHessianBlockAdj ( const HCL_Vector_d &, const HCL_Vector_d &, const HCL_Vector_d &, int i, int j, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const CheckHessianBlockAdj calls CheckHessianBlock to test the correctness of the (i,j) block of the Hessian, and then calls the HCL_LinearOp_d method CheckAdj to test the correctness of the adjoint of the block |
| | Write ( ostream & str ) const Debugging information |
| | Value1 ( const HCL_Vector_d & x ) const Value1 computes the value of 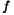 at at 
|
| | PartialGradient1 ( int i, const HCL_Vector_d & x, HCL_Vector_d & y ) const PartialGradient1 computes the gradient of 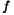 at at  with
respect to the with
respect to the 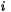 th component of th component of 
|
| | HessianBlock1 ( int i, int j, const HCL_Vector_d & x ) const HessianBlock1 computes the 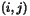 block of the Hessian of block of the Hessian of
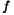 at at 
|
| | HessianBlockImage ( int i, int j, const HCL_Vector_d & x, const HCL_Vector_d & dx, HCL_Vector_d & dy ) const HessianBlockImage computes the image of the 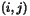 block of
the Hessian of block of
the Hessian of 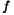 at at  , acting on , acting on 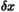
|
HCL_FunctionalProductDomain_d is an abstract base class used to represents functionals defined on product spaces. That is, this class represents a functional of the formwhere
The gradient and Hessian of such a function can be expressed in terms of partial derivatives; Therefore, the basic methods of this class are Value, PartialGradient, and HessianBlock. Value1 computes
, PartialGradient computes the gradient of
with respect to one of the components of
, and HessianBlock computes a block of the Hessian corresponding to one of the second partial derivatives of
. To be precise, the
partial gradient of
is defined by
where
is the partial derivative of
with respect to the
th component of
. Similarly,
defines the
block of the Hessian.
HCL_FunctionalProductDomain_d is derived from HCL_Functional_d. As in the case of an ordinary functional represented by a class derived from HCL_Functional_d, an evaluation class is defined to represent the triple
. The documentation for HCL_Functional_d, as well as the report "Implementing functionals in HCL", Technical Report 99-24, Department of Computational and Applied Mathematics, Rice University, PO Box 1892, Houston, TX 77251-1892. should be consulted for general information about functionals, including the rationale for the existence of the evaluation class. The implementor of a derived class need not implement a separate class to represent the evaluation object if there is no efficiency gain in doing so. By implementing the protected virtual functions Value1, PartialGradient1, and HessianBlock1 or HessianBlockImage, the use of the default evaluation class HCL_FunctionalProductDomainDefaultEval_d is enabled.
A forthcoming report, "Implementing HCL functionals and operators on product spaces", will explain in detail the different models for implementing derived classes. This report should be available in early 2000 from the Rice University address given above.
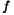 at
at  .
If Value1, PartialGradient1, and HessianBlock1
or HessianBlockImage are implemented, then the default
implementation of the Evaluate method can be used. This
creates an instance of
HCL_FunctionProductDomainDefaultEval_d.
.
If Value1, PartialGradient1, and HessianBlock1
or HessianBlockImage are implemented, then the default
implementation of the Evaluate method can be used. This
creates an instance of
HCL_FunctionProductDomainDefaultEval_d.
![]() virtual void PartialGradient1( int i, const HCL_Vector_d & x, HCL_Vector_d & y ) const
virtual void PartialGradient1( int i, const HCL_Vector_d & x, HCL_Vector_d & y ) const
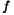 at
at  with
respect to the
with
respect to the 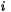 th component of
th component of  . If Value1,
PartialGradient1, and HessianBlock1 or
HessianBlockImage are implemented, then the default
implementation of the Evaluate method can be used. This
creates an instance of
HCL_FunctionProductDomainDefaultEval_d.
. If Value1,
PartialGradient1, and HessianBlock1 or
HessianBlockImage are implemented, then the default
implementation of the Evaluate method can be used. This
creates an instance of
HCL_FunctionProductDomainDefaultEval_d.
![]() virtual HCL_LinearOp_d* HessianBlock1( int i, int j, const HCL_Vector_d & x ) const
virtual HCL_LinearOp_d* HessianBlock1( int i, int j, const HCL_Vector_d & x ) const
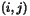 block of the Hessian of
block of the Hessian of
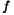 at
at  . If Value1, PartialGradient1, and
HessianBlock1 or HessianBlockImage are implemented,
then the default implementation of the Evaluate method can be
used. This creates an instance of
HCL_FunctionProductDomainDefaultEval_d.
. If Value1, PartialGradient1, and
HessianBlock1 or HessianBlockImage are implemented,
then the default implementation of the Evaluate method can be
used. This creates an instance of
HCL_FunctionProductDomainDefaultEval_d.
![]() virtual void HessianBlockImage( int i, int j, const HCL_Vector_d & x, const HCL_Vector_d & dx, HCL_Vector_d & dy ) const
virtual void HessianBlockImage( int i, int j, const HCL_Vector_d & x, const HCL_Vector_d & dx, HCL_Vector_d & dy ) const
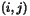 block of
the Hessian of
block of
the Hessian of 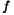 at
at  , acting on
, acting on 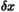 . If Value1,
PartialGradient1, and HessianBlock1 or
HessianBlockImage are implemented, then the default
implementation of the Evaluate method can be
used. This creates an instance of
HCL_FunctionProductDomainDefaultEval_d.
. If Value1,
PartialGradient1, and HessianBlock1 or
HessianBlockImage are implemented, then the default
implementation of the Evaluate method can be
used. This creates an instance of
HCL_FunctionProductDomainDefaultEval_d.
![]() virtual HCL_VectorSpace_d& Domain() const
virtual HCL_VectorSpace_d& Domain() const
![]() virtual HCL_ProductSpace_d& ProductDomain() const
virtual HCL_ProductSpace_d& ProductDomain() const
![]() virtual HCL_EvaluateFunctional_d* Evaluate( const HCL_Vector_d & x ) const
virtual HCL_EvaluateFunctional_d* Evaluate( const HCL_Vector_d & x ) const
![]() virtual void PartialGradient( int i, const HCL_Vector_d & x, HCL_Vector_d & g ) const
virtual void PartialGradient( int i, const HCL_Vector_d & x, HCL_Vector_d & g ) const
![]() virtual HCL_LinearOp_d* HessianBlock( int i, int j, const HCL_Vector_d & x ) const
virtual HCL_LinearOp_d* HessianBlock( int i, int j, const HCL_Vector_d & x ) const
![]() int CheckHessianBlock( const HCL_Vector_d &, const HCL_Vector_d &, const HCL_Vector_d &, int i, int j, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const
int CheckHessianBlock( const HCL_Vector_d &, const HCL_Vector_d &, const HCL_Vector_d &, int i, int j, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const
![]() int CheckHessianBlock( const HCL_Vector_d &, const HCL_Vector_d &, int ind, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const
int CheckHessianBlock( const HCL_Vector_d &, const HCL_Vector_d &, int ind, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const
![]() int CheckHessianBlockAdj( const HCL_Vector_d &, const HCL_Vector_d &, const HCL_Vector_d &, int i, int j, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const
int CheckHessianBlockAdj( const HCL_Vector_d &, const HCL_Vector_d &, const HCL_Vector_d &, int i, int j, ostream & str, int n=10, double hmin=0.1, double hmax=1.0 ) const
![]() virtual ostream& Write( ostream & str ) const
virtual ostream& Write( ostream & str ) const
alphabetic index hierarchy of classes

this page has been generated automatically by doc++
(c)opyright by Malte Zöckler, Roland Wunderling
contact: doc++@zib.de