 class HCL_LineSearch_DS_d : public HCL_LineSearch_d
class HCL_LineSearch_DS_d : public HCL_LineSearch_d  class HCL_LineSearch_DS_d : public HCL_LineSearch_d
class HCL_LineSearch_DS_d : public HCL_LineSearch_d An implementation of a backtracking line search algorithm using cubic interpolation (See Dennis and Schnabel, "Numerical Methods for Unconstrained Optimization and Nonlinear Equations", Prentice-Hall (1983))
| | HCL_LineSearch_DS_d ( char *fname = NULL ) Usual constructor |
| | Parameters () const Access to the parameter table |
| | SetScaling ( const HCL_LinearOp_d * S ) SetScaling allows the specification of a different inner product (and hence norm) |
| | UnSetScaling () UnSetScaling causes the line search to use the default inner product |
| | Search ( HCL_Functional_d & fptr, const HCL_Vector_d & xcur, HCL_Vector_d & xnext, HCL_Vector_d & dir, HCL_EvaluateFunctional_d * xinit_eval) LineSearch algorithm |
| | Write ( ostream & str ) const Prints description of the object |
Term codes
An implementation of a backtracking line search algorithm using cubic interpolation (See Dennis and Schnabel, "Numerical Methods for Unconstrained Optimization and Nonlinear Equations", Prentice-Hall (1983)).The description of this class differs from the description of the base class HCL_LineSearch_d in only one regard: the second criteria for defining an acceptable step is
This prevents short steps by requiring that the slope be increased from its initial (negative) value, although it does not require that the step reach an approximate minimizer. This criterion is sufficient to allow a positive definite update in a BFGS algorithm.
![]() double MinStep
double MinStep
![]() double MaxStep
double MaxStep
![]() int MaxSample
int MaxSample
![]() double ZeroDivideTol
double ZeroDivideTol
![]() int DispFlag
int DispFlag
![]() int DumpFlag
int DumpFlag
![]() char DumpFile[81]
char DumpFile[81]
![]() int DispPrecision
int DispPrecision
![]() int DumpPrecision
int DumpPrecision
![]() double BracketIncrease
double BracketIncrease
![]() int MaxTkn
int MaxTkn
![]() virtual Table& Parameters() const
virtual Table& Parameters() const
![]() virtual void SetScaling( const HCL_LinearOp_d * S )
virtual void SetScaling( const HCL_LinearOp_d * S )
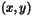 , the scaled inner
product
, the scaled inner
product 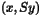 will be used, where
will be used, where 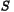 is a symmetric
positive definite operator. Through this method, a line
search can be made consistent with a minimization algorithm which
scales the norm.
is a symmetric
positive definite operator. Through this method, a line
search can be made consistent with a minimization algorithm which
scales the norm.
![]() virtual void UnSetScaling()
virtual void UnSetScaling()
![]() virtual HCL_EvaluateFunctional_d* Search( HCL_Functional_d & fptr, const HCL_Vector_d & xcur, HCL_Vector_d & xnext, HCL_Vector_d & dir, HCL_EvaluateFunctional_d * xinit_eval)
virtual HCL_EvaluateFunctional_d* Search( HCL_Functional_d & fptr, const HCL_Vector_d & xcur, HCL_Vector_d & xnext, HCL_Vector_d & dir, HCL_EvaluateFunctional_d * xinit_eval)
xcur - starting point, on successful completion, this will hold
the computed minimum
dir - starting direction
xinit_eval - evaluation object for starting point![]() virtual ostream& Write( ostream & str ) const
virtual ostream& Write( ostream & str ) const
alphabetic index hierarchy of classes

this page has been generated automatically by doc++
(c)opyright by Malte Zöckler, Roland Wunderling
contact: doc++@zib.de