class HCL_RestrictedBiLinearOp_d : public HCL_LinearOp_d

HCL_RestrictedBiLinearOp_d creates one of the three linear operators related to a bilinear operator

Inheritance:

Public Methods

HCL_RestrictedBiLinearOp_d ( const HCL_BiLinearOp_d * t, int of, const HCL_Vector_d & v )
Usual constructor; needs a pointer to the underlying bilinear operator, a flag indicating which restricted operator is to be represented (1, 2, or 3), and the fixed vector
virtual HCL_VectorSpace_d& Domain () const
Domain space access
virtual HCL_VectorSpace_d& Range () const
Range space access
virtual void Image ( const HCL_Vector_d & x, HCL_Vector_d & y ) const
Image compute the action of the operator on x, giving y.
virtual void AdjImage ( const HCL_Vector_d & y, HCL_Vector_d & x ) const
AdjImage computes the action of the adjoint on y, giving x
virtual void InvImage (const HCL_Vector_d & y, HCL_Vector_d & x) const
InvImage computes the action of the inverse on y, giving x
virtual void InvAdjImage (const HCL_Vector_d & x, HCL_Vector_d & y) const
InvAdjImage computes the action of the inverse adjoint on x, giving y
virtual ostream& Write ( ostream & str ) const
Write invokes the Write method of the underlying bilinear operator

Inherited from HCL_LinearOp_d:

Public Methods

int CheckAdj(int Display = 1, double tol = 1000 )
virtual void NormalImage( const HCL_Vector_d & x, HCL_Vector_d & z ) const
int CheckNormal( int display = 1, double tol = 100 )
virtual void ImageAdd(const HCL_Vector_d & x, const HCL_Vector_d & z, HCL_Vector_d & y, double a=1.0, double b=1.0) const
virtual void AdjImageAdd(const HCL_Vector_d & x, const HCL_Vector_d & z, HCL_Vector_d & y, double a=1.0, double b=1.0) const
virtual void NormalImageAdd(const HCL_Vector_d & x, const HCL_Vector_d & z, HCL_Vector_d & y, double a=1.0, double b=1.0) const
virtual void InvImageAdd(const HCL_Vector_d & x, const HCL_Vector_d & z, HCL_Vector_d & y, double a=1.0, double b=1.0) const
virtual void InvAdjImageAdd(const HCL_Vector_d & x, const HCL_Vector_d & z, HCL_Vector_d & y, double a=1.0, double b=1.0) const
virtual void ImageAdd(const HCL_Vector_d & x, HCL_Vector_d & y, double a=1.0, double b=1.0) const
virtual void AdjImageAdd(const HCL_Vector_d & x, HCL_Vector_d & y, double a=1.0, double b=1.0) const
virtual void NormalImageAdd(const HCL_Vector_d & x, HCL_Vector_d & y, double a=1.0, double b=1.0) const
virtual void InvImageAdd(const HCL_Vector_d & x, HCL_Vector_d & y, double a=1.0, double b=1.0) const
virtual void InvAdjImageAdd(const HCL_Vector_d & x, HCL_Vector_d & y, double a=1.0, double b=1.0) const

Inherited from HCL_Base:

Public Methods

void IncCount() const
void DecCount() const
int Count() const

Documentation

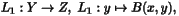
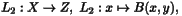
HCL_RestrictedBiLinearOp_d creates one of the three linear operators related to a bilinear operator. Suppose is a bilinear operator represented by an instance of HCL_BiLinearOp_d. The three related operators are Note that to define , a fixed x in X is required; similarly y in Y defines , and z in Z defines . Note also that the fourth natural operator, turns out to be the adjoint of .

This class is concrete: all of its methods are implemented.

HCL_RestrictedBiLinearOp_d( const HCL_BiLinearOp_d * t, int of, const HCL_Vector_d & v )
Usual constructor; needs a pointer to the underlying bilinear operator, a flag indicating which restricted operator is to be represented (1, 2, or 3), and the fixed vector. Note that an independent copy of the fixed vector is made.

virtual HCL_VectorSpace_d& Domain() const
Domain space access. Returns a reference to the domain of the operator, which is an HCL_VectorSpace_d.

virtual HCL_VectorSpace_d& Range() const
Range space access. Returns a reference to the range of the operator, which is an HCL_VectorSpace_d.

virtual void Image( const HCL_Vector_d & x, HCL_Vector_d & y ) const
Image compute the action of the operator on x, giving y.

virtual void AdjImage( const HCL_Vector_d & y, HCL_Vector_d & x ) const
AdjImage computes the action of the adjoint on y, giving x

virtual void InvImage(const HCL_Vector_d & y, HCL_Vector_d & x) const
InvImage computes the action of the inverse on y, giving x. This method is implemented to return an error message.

virtual void InvAdjImage(const HCL_Vector_d & x, HCL_Vector_d & y) const
InvAdjImage computes the action of the inverse adjoint on x, giving y. This method is implemented to return an error message.

virtual ostream& Write( ostream & str ) const
Write invokes the Write method of the underlying bilinear operator

This class has no child classes.

alphabetic index hierarchy of classes

this page has been generated automatically by doc++

(c)opyright by Malte Zöckler, Roland Wunderling
contact: doc++@zib.de